

pythonで3Dグラフを作ってみたい!
今回は、このような人向けにpythonを用いて様々な形の3Dグラフの作成方法をご紹介していこうと思います。
初心者の方でもわかりやすいように丁寧に説明しているので、ぜひ最後まで見ていってください。
この記事でわかること
- 3D空間における関数グラフの作成
- 3D空間における散布図の作成
- 3D空間における棒グラフの作成
目次
グラフ作成の準備

実際に3Dグラフを作成するためには準備が必要です。
ということで、ここからは具体的なコードを用いて説明していきます。
実際に自分でも動作を確かめて、理解を深めていきましょう!
必要なライブラリのインポート
今回使用するライブラリは、numpyとmatplotlibです。
下記コードを記述してインポートしていきます。
import numpy as np
import matplotlib.pyplot as pltここで、numpy・matplotlibって何?という方は、ぜひ下記の記事を参考にしてみてください。
それぞれのライブラリの説明と、使い方を初心者の方でもわかりやすいように紹介しています。
関連記事はこちら!
これで今回行う下準備は完了です。
早速3Dグラフ作成の方に移っていきましょう。
3Dグラフの作成

では、実際に3Dグラフを作成していこうと思います。
3Dグラフと一口に言っても様々な形があり、本記事では複数のグラフを紹介しているので、ぜひ参考にしてみてください。
3D関数グラフ
まず一つ目は、3Dの関数グラフです。
実際のコードを見ながら説明していこうと思います。
<input>
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8)) #図のサイズを決定
ax = fig.add_subplot(projection='3d') #3d空間の作成
z = np.arange(0, 10, 0.01) #0~9.99まで0.01刻みでzに代入
x = np.cos(z)
y = np.sin(z)
#各軸に対するラベルの作成
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.plot(x,y,z)
plt.show()<output>
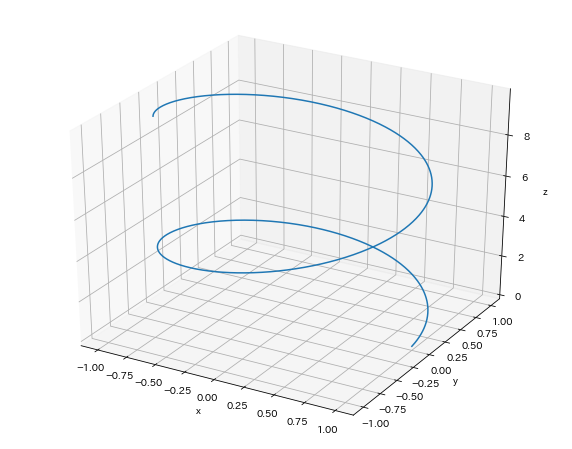
関数plt.figure()でグラフを張り付ける図のサイズを指定し、関数fig.add_subplot()で3D空間を作成するといった処理になっています。
ちなみに、関数の色指定やラインスタイルの指定は2Dの時と同様に行うことが出来るので、興味のある方は試してみましょう。
3D散布図
続いて、散布図の作成方法についてです。
<input>
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8)) #図のサイズを決定
ax = fig.add_subplot(projection='3d') #3d空間の作成
x = np.random.randn(100) #標準正規分布に従って乱数を生成する
y = np.random.randn(100)
z = np.random.randn(100)
#各軸に対するラベルの作成
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.scatter(x,y,z)
plt.show()<output>
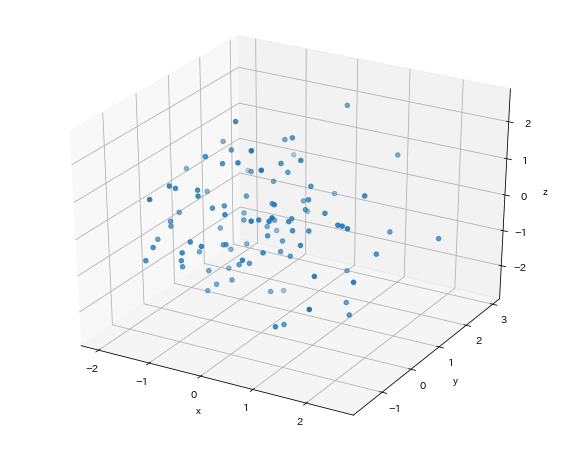
x,y,zに乱数を代入して点を100個プロットしているといった感じです。
今回は、関数random.randn()を使用したので、おおよその要素が-2~2の間に収まっています。
3D棒グラフ
次は、3D棒グラフです。
先ほどまでと異なり、あまり見たことのない関数もいくつか含まれていると思うので、丁寧に説明していこうと思います。
<input>
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8)) #図のサイズを決定
ax = fig.add_subplot(projection='3d') #3d空間の作成
x = [1,2]
y = [3,4]
x2,y2 = np.meshgrid(x,y) #格子状の二次元配列作成(後ほど補足説明あり)
x3 = x2.ravel() #多次元配列を一次元に変更(後ほど補足説明あり)
y3 = y2.ravel() #多次元配列を一次元に変更
height = [1,2,3,4] #各棒グラフの高さ設定
bottom = np.ones_like(height) #1のみで構成された配列を作成。要素数はheightと同じ
width = 0.2 #各棒グラフの横幅設定
depth = 0.2 #各棒グラフの奥行き設定
#各軸に対するラベルの作成
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.bar3d(x3,y3,bottom, width, depth, height) #3D棒グラフの生成
plt.show()<output>
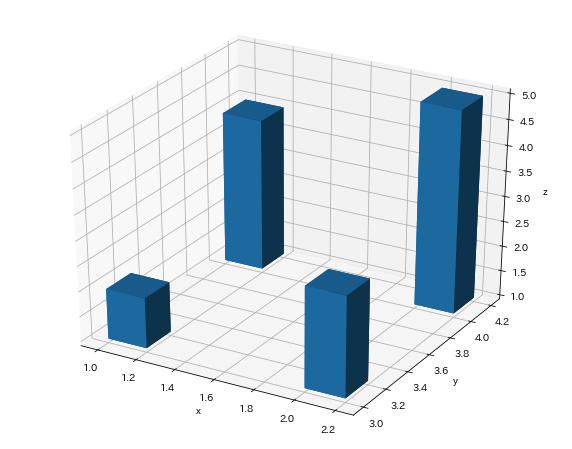
いくつかの関数について以下の表を用いて説明しています。
コードを見てもよくわからない部分がある方は表を参考にしてください。
また、『np.meshgrid()』と『ravel』に関しては、言葉のみの説明だとわかりにくいので、次の項目で個別にコードを使いながら説明していこうと思います。
| 関数 | 説明 |
|---|---|
| np.meshgrid() | 後ほど補足説明 |
| ravel() | 後ほど補足説明 |
| np.ones_like(x) | 配列xと同じ要素数で、すべての要素が1の配列を作成する関数。 例えば、配列xが[1,2,3,4]ならば、この関数によって作成される配列は、[1,1,1,1]である。 |
| ax.bar3d(x,y,bottom,width,depth,height) | 三次元の棒グラフを生成するための関数。 引数が多いので、以下で個別に引数の説明を行う。 ・x,y:棒グラフの開始位置を指定する引数 ・bottom:棒グラフの底を指定する引数。今回はすべて1となっており、実際に関数を見ると、z=1.0から 棒グラフが生成されていることがわかる。 ・width,depth,height:棒グラフのサイズを指定する引数。widthは横幅、depthは奥行き、heightは高さとなっている。 |
【補足】np.meshgrid()とravel()について
ここでは、先ほどの3D棒グラフのコード内に登場した、np.meshgrid()とravel()の補足説明を行います。
<input>
import numpy as np
x = [1,2]
y = [3,4]
x2,y2 = np.meshgrid(x,y) #格子状のn次元配列作成
x3 = x2.ravel() #n次元配列を一次元に変更
y3 = y2.ravel() #n次元配列を一次元に変更
print("np.meshgridの出力")
print(x2)
print(y2)
print("ravelの出力")
print(x3)
print(y3)<output>
np.meshgridの出力
[[1 2]
[1 2]]
[[3 3]
[4 4]]
ravelの出力
[1 2 1 2]
[3 3 4 4]まず、meshgridですがご覧の通り、多次元配列を作成する関数となっています。
どのような多次元配列かと言いますと、x2にはxの配列を多次元化したもの、y2にはyの配列を多次元化したものが入るといった感じです。
ちなみに、今回はxとyの要素数が2なので二次元配列が作成されていますが、xとyの要素数を変更するとそれに応じてx2やy2の次元数も異なるものになるので押さえておきましょう。
また、ravelですが、こちらは多次元配列を一次元に変換するための関数になっています。
出力結果は上記の通りです。
3D球面(球体)
3Dグラフが作成できるということは、円のみでなく球体も作ることが出来るんです。
ちなみに、知らない人も多いと思うのですが、球体の方程式はこんな感じです。
原点中心で半径が r であるような球体は,媒介変数θ、φ (ただし、0≤θ≤π,0≤ϕ<2π)を用いて以下のように表せる:
x=rsinθcosϕ
y=rsinθsinϕ
z=rcosθ
この式を参考にコードを記述していきます。
<input>
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8)) #図のサイズを決定
ax = fig.add_subplot(projection='3d') #3d空間の作成
x = np.linspace(0, np.pi, 200) #0~πまでの数値を等間隔で刻んで200個、xに代入
y = np.linspace(0, 2*np.pi, 100) #0~2πまでの数値を等間隔で刻んで100個、yに代入
x2,y2 = np.meshgrid(x,y) #格子状の多次元配列作成
#球の公式(a = 半径、x2 = θ、y2 = φ)
a = 5
X = a * np.sin(x2) * np.cos(y2)
Y = a * np.sin(x2) * np.sin(y2)
Z = a * np.cos(x2)
#各軸に対するラベルの作成
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.plot_surface(X,Y,Z, cmap='winter') #球面のグラフ作成
plt.show()<output>
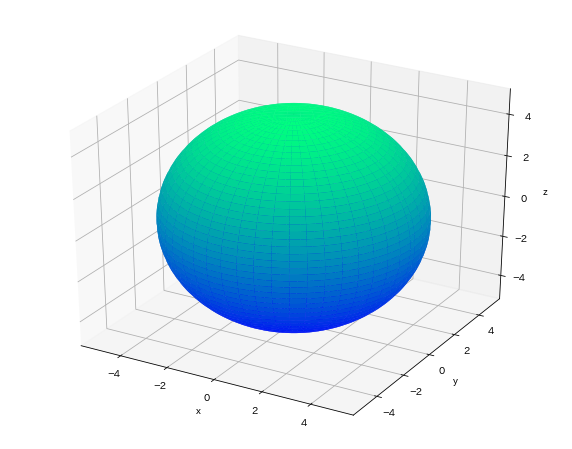
新しく使用した関数は特にないので、関数に関する説明はコードのコメントを参考にしていただければと思います。
また、今回はcolormapにwinterを設定しています。
ずっと青だとなんか飽き飽きするので、気分転換に少し色を変えてみました。
colormapは調べてみるとかなりの種類あるので、ぜひいろいろな図形に対して試してみましょう。
ワイヤーフレーム
続いて、同じ球体のワイヤーフレーム生成方法についてご紹介いたします。
<input>
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8)) #図のサイズを決定
ax = fig.add_subplot(projection='3d') #3d空間の作成
x = np.linspace(0, np.pi, 200) #0~πまでの数値を等間隔で刻んで200個、xに代入
y = np.linspace(0, 2*np.pi, 100) #0~2πまでの数値を等間隔で刻んで100個、yに代入
x2,y2 = np.meshgrid(x,y) #格子状の多次元配列作成
#球の公式(a = 半径、x2 = θ、y2 = φ)
a = 5
X = a * np.sin(x2) * np.cos(y2)
Y = a * np.sin(x2) * np.sin(y2)
Z = a * np.cos(x2)
#各軸に対するラベルの作成
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.plot_wireframe(X,Y,Z, color = 'black') #wireframeを生成
plt.show()<output>
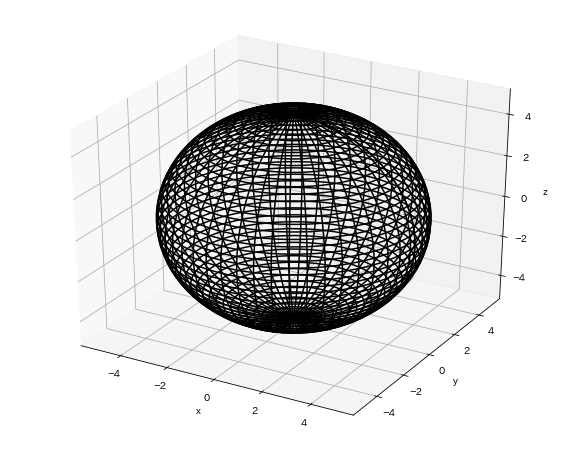
球体をワイヤーフレームに変更するためには、先ほどの球体を作る関数『plot_surfae()』を『plot_wireframe()』に変えてあげればよいだけです。それ以外は特にコードをいじることなく変更することが出来ます。
ちなみに、今回はワイヤーが見やすいようにcolorを黒に変えてみました。
矢印(ベクトル)
最後に、ベクトルで構成されているグラフの生成方法についてです。
まずはコードを見ていきましょう。
<input>
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,8)) #図のサイズを決定
ax = fig.add_subplot(projection='3d') #3d空間の作成
z = np.arange(0, 10, 0.3) #0~9.99まで0.3刻みでzに代入
x = np.cos(z)
y = np.sin(z)
u = -x
v = -y
w = -z
#各軸に対するラベルの作成
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.quiver(x,y,z,u,v,w,normalize=True,color='blue') #ベクトルを用いたグラフの生成
plt.show()<output>
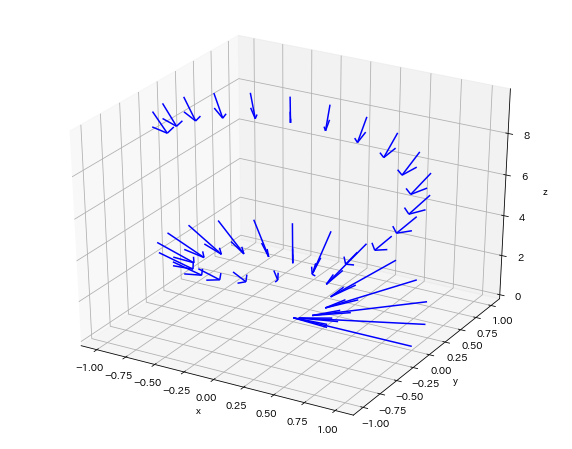
ベクトルを用いたグラフの生成ということで、グラフの形は最初の3D関数グラフをそのまま持ってきています。
また、コードを見てわかる通り関数quiver()がベクトルを用いたグラフの生成を行っています。
関数quiver()に関しては引数が非常に多いので、以下の表にて各変数の説明を行います。
参考にしてください。
| 引数 | 説明 |
|---|---|
| x,y,z | 矢印が構成するグラフの形を指定する引数。 通常の関数グラフと指定の仕方は全く同じ。 |
| u,v,w | それぞれのベクトルのx成分、y成分、z成分を指定する引数。 よくわからない人は、矢印(ベクトル)の向きを指定していると思っていればOK。 |
| normalize | normalize=Trueとすることで、各ベクトルの正規化を行っている。 正規化とは、ベクトルの矢印の向きを維持しつつ、長さを1に変換することである。 これにより、すべてのベクトルの長さがそろうことになる。(奥行き等の関係で長さが一定に見えませんが) |
| color | 色を指定する引数 |
まとめ
今回は、さまざまな形の3Dグラフを作成していきましたが、いかがだったでしょうか。
3Dグラフは2Dより複雑なだけあって初めて作った際にはなんか達成感が出ますよね。
もちろん本日紹介したものがすべてではなく、本記事の知識を持っていれば、もっと多くの図形を生成することが出来ます。
試しに自分の好きな図形を作ってみてはどうでしょうか。